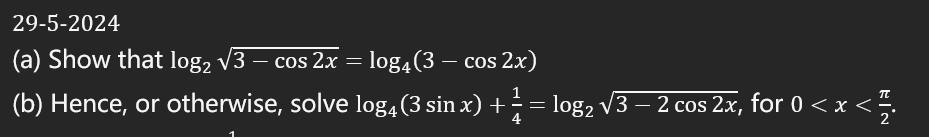Everyday maths - 400*5+12*2

[HappyCod]

Question I posted somewhere:

[HappyCod]

22nd October 2024:

[32294]

Answer

I solved it, but you should solve it yourself. Come back tomorrow.
My disappointment in you is immeasurable.

a = 400

[HappyCod]

Oh yeah, you don’t need calculator for solving logarithm in the first question of 22nd Oct.

Using calculator to find the square of 2023 and 1977 in 1st June question isn’t necessary too.

[32294]

Answer

1. too lazy, remind me to finish my solution later

2. 
a = 0
b = -3

edit: just noticed cod posted the solution for #2 already, i am blind.

[HappyCod]

Reminder reminder reminder.

[32294]

Answer

1. Still too lazy, remind me in a few years

[HappyCod]

lol
4 minutes still considered “in” a few years XD

[HappyCod]

29th May 2024 (Question posted somewhere):

[HappyCod]

Answer of question 1

Question 1 of the year

Actually I did not mean to post the answer for question kind of proving L.H.S. = R.H.S. , but, welp, the first person trying to solve it got the steps wrong, and maybe people need to check their answers too, so it is here now.

[HappyCod]

Answer for 1st June 2024: 400

[HappyCod]

Answer for 22nd October:

[KielleAzomas11]

Just a Nice Trivia, and tbh, its looks intimidating at first, but really, its all algebra stuffs, one basic derivation, and some assumptions.

Formula of SPEED OF SOUND:

Base formulas that we’ll need:

• Density Formula (ρ):
  ρ = mass/volume = m/V

• Force Formula (F):
  F = mass * acceleration = ma

• Velocity and Acceleration concept (a):
  v = change in distance / change in time = dx/dt
  a = change in Velocity / change in time = dv/dt

• Pressure Formula (p):
  p = Force/Area = F/A

• Continuity equation:
  

• Summation of Forces over an area/sound wave:
  

  

• Adiabatic process:
  

• Ideal Gas Law:
  
  *this is a bit of a oversimplification but ya can treat “n” as mass here

==============================================================

Assumptions:

• Main medium is Air,
  thus Compressible

• Assume Air is an Ideal Gas/Fluid
  and Friction can be neglected

• No change in Working Area:
  Area in = Area out

• A sound wave/barrier will always form,
  Thus, we will have a difference of properties (mainly pressure, temperature, and density) between the front and back of the barrier

• 1st law of thermodynamics:
  Energy can neither be created or destroyed, thus it needs to be conserved on either side of the sound wave.
  *Also applies to mass of the fluid

• If the output value is very very very Little,
  Then it can be safely Neglected

• Adiabatic Process (No transfer/changes in heat from or to the surrounding environment)

|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| SOLUTION ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Click here for the solution and heavily simplified explanation

Start with Continuity Equation along a given sound wave:

but since the fluid is compressible (ρ changes) and Area is constant;
Velocity “v” (which in this case, is the speed of sound) needs to adjust for the sake of conservation of mass

thus we get:

ρAv = (ρ + dρ)(A)(v + dv)

but since Area is constant;

ρv = (ρ + dρ)(v + dv)

expand:

ρv = ρv + ρ(dv) + (dρ)v + (dρ)(dv)
0 = ρ(dv) + (dρ)v + (dρ)(dv)

but since (dρ)(dv) results in very very very Little value, it can be safely neglected;

0 = ρ(dv) + (dρ)v

Let’s Hold on to this for now…

==============================================================

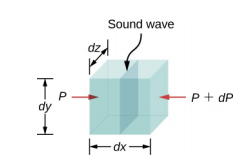
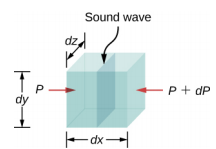
Next is the Summation of Forces along a infinitesimal volume of the fluid as the Sound wave travel:

*Back → Front

Thus,

F total = F back + F front

Substitute the Force formula on the left and Pressure Formula on the right:

m(a) = p(A) + (p + dp)(A)

but since ρ = m/V and referig to the figure above, A = (dy)(dz)

ρ(V)(a) = p(dy)(dz) − (p + dp)(dy)(dz)
*careful when distinguishing density “ρ” and pressure “p”

referring again on the figure above, V = (dx)(dy)(dz). Also, expand the right side:

ρ(dx)(dy)(dz)(a) = pdydz − pdydz − dpdydz
ρ(dx)(dy)(dz)(a) = − dpdydz

now isolate the acceleration:

a = − ( (dp)(dy)(dz) / ρ(dx)(dy)(dz) )

Simplify:

a = − dp / ρ(dx)

since a = dv/dt and v = dx/dt:

dv/dt = − dp / ρ(dx)
dv (dx/dt) = − dp / ρ
v(dv) = − dp / ρ

Rearrange and Finally we have:

ρ(dv) = − dp / v

Now Let’s incorporate the “0 = ρ(dv) + (dρ)v” formula from before…

==============================================================

0 = ρ(dv) + (dρ)v

since ρ(dv) = − dp / v, then:

0 = (− dp / v) + (dρ)v
dp / v = v(dρ)
v^2 = dp / dρ
v = sqrt( dp / dρ )

This states that the speed of sound depends on the changes of density and pressure between back and front of the sound wave.

But we’re halfway there bros and gals, this formula doesn’t really tell us a definite value since practically speaking, density is very difficult to measure in the real world let alone measure both front and back of the sound wave…

Let’s hold on this formula once again for the time being…

==============================================================

Ok, now for the single basic derivation of the whole process:

using the Adiabatic Process:

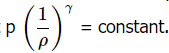
lets separate pressure and density and derive with respect to density:

p = c (ρ^γ)
(d/dρ)(p) = (d/dρ) c(ρ^γ)
dp/dρ = c(γ)((ρ^(γ-1))

now let’s substitute the c = p / (ρ^γ) back and simplify:

dp/dρ = ( p / (ρ^γ) ) (γ)( ρ^(γ-1) )
dp/dρ = γ ( p / ρ )

Now incorporate it to the formula we’ve hold on

==============================================================

v = sqrt( dp / dρ ) = sqrt( γ ( p / ρ ))

This formula now tells us that the speed of sound basically depends on the “γ” constant that varies from fluid to fluid, pressure of the fluid, and the density of the fluid.

But as stated, Density is Very difficult to measure in the real world, thus we need a more reliable way of measuring the speed of sound.

Here comes the Ideal Gas Law to simplify things further (its also a very complicated topic as to why it makes sense so let’s just accept it for now XD):

pV = mRT
or
p = ρRT
p / ρ = RT

Incorporating these formula together and we’ll have:

v = sqrt( γRT )

Which basically states that the speed of sound varies with the constants “γ” and “R” which varies on the type of medium/fluid, and Temperature of the fluid.

and that’s it, we’ve successfully derived a Speed of Sound Formula with just a single variable “Temperature” (as long as we know the “γ” and “R” of the medium/fluid. These are also a topic on its own but basically these just defines how energy flows and works on these fluids).

Thus, Speed of sound varies only with Temperature (and the type of Fluid)

==============================================================

BONUS:

For measuring Mach numbers:

M = local velocity of the object / speed of sound
M = v / sqrt( γRT )

Note: I just find this facinating and wanted to share with ya’ll. Happy Learning and Drink water \o/

A good reference if you want to dive deeper

[32294]

Real question on my college trig homework.
You need mental help if you get it wrong.

[KielleAzomas11]

hmmmmm… maybe one of the others except the circle

[32294]

To hopefully noone’s surprise:

It is a circle.